Das äußere Feld eines elektrisch geladenen Körpers kann näherungsweise durch Superposition endlich vieler elektrischer Ladungsträger berechnet werden, die sich in einer Gleichgewichtslage auf dessen Oberfläche befinden. Diese Gleichgewichtslage ist durch ein Minimum der elektrostatischen Energie des Systems charakterisiert. Infolge langsamer Konvergenz der überlagerten Punktpotentiale gegen das elektrostatische Potential im Außenraum des geladenen Körpers (~ 1/√n, n: Zahl der Ladungsträger), ist diese Methode in ihrer ursprünglichen Form nicht konkurrenzfähig gegenüber anderen Verfahren zur numerischen Feldberechnung, wie z.B. Randintegralmethoden.
Eine Analyse zeigt, dass der größte Fehleranteil dadurch entsteht, dass bei der Berechnung des Potentials einer endlichen Ladungsverteilung die Energie der Ladungsträger in ihrem eigenen Feld unendlich wäre und nicht berücksichtigt werden kann.
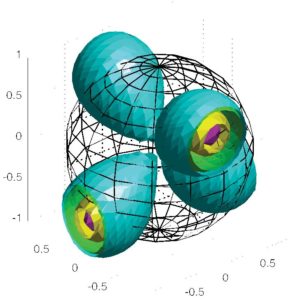
Ziel ist es, ein alternatives Extremalpunktsystem einzuführen, das ein abgewandeltes diskretes Potential minimiert, das so modifiziert wurden, dass das Potential der kontinuierlichen Ladungsverteilung um Größenordnungen schneller approximiert wird.
Die zugrunde liegende Idee ist, die approximierende Punktewolke in zwei Klassen zu unterteilen, und nur Wechselwirkungen zwischen „Ladungen“ der unterschiedlichen Klassen zu berücksichtigen. Über geometrische Dualität der beiden Klassen wird sichergestellt, dass die Punkte jeder Klasse eine gute Verteilung besitzen. Ein zweidimensionales Analogon dieser Methode wurde bereits im letzten Jahrhundert von K. Menke untersucht. In letzterem Fall konnte ein schnelles asymptotisches Abklingen des Fehlers auf glatten Kurven in der Größenordnung mit nachgewiesen werden. Bei dieser Konvergenzgeschwindigkeit genügen wenige Punkte, um das äußere Feld genau darzustellen, so dass dieses Vorgehen als formale Methode zur numerischen Feldberechnung effizient einsetzbar wird.
Dabei beschränkt sich der Einsatz von Extremalpunktmethoden keineswegs auf statische Probleme: Durch die Erweiterung der Minimierungsaufgabe zur Bestimmung der Extremalpunkte um ein zusätzliches zeitabhängiges externes Feld ist es möglich, eine Kopplung transienter Effekte innerhalb des umschlossenen Volumens mit dem äußeren Feld zu berücksichtigen. Insbesondere ist die Kopplung einer transienten Finite-Elemente-Simulation innerhalb des Volumens mit der Extremalpunktmethode aussichtsreich.
Literatur
Kontakt : Manuel Jaraczewski
Letzte Änderung: 2. November 2017